Calculus Optimization

🚀 ปลดล็อกพลังแคลคูลัส: หาจุดสูงสุดของปริมาตรกล่องได้ด้วยคณิตศาสตร์!

เรียนรู้ concept ยากๆ ให้เข้าใจง่ายด้วย Interactive Visuals จาก Panya AI Tutor

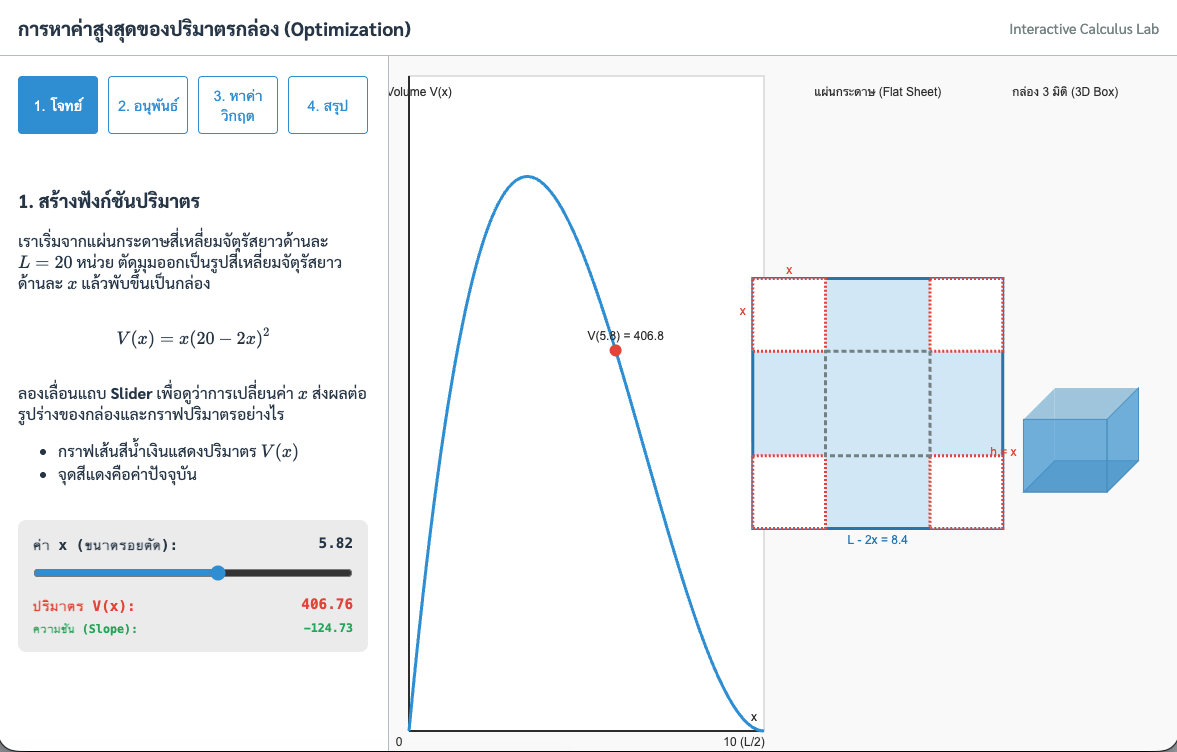
ภาพจำลองโจทย์: ด้านซ้ายคือแผ่นกระดาษต้นแบบ เมื่อเราทดลองเลื่อน Slider เพื่อปรับขนาดรอยตัด ($x$) จะเห็นการเปลี่ยนแปลงของรูปทรงกล่องและกราฟปริมาตรไปพร้อมๆ กัน

เคยสงสัยไหมว่านักวิทยาศาสตร์หาจุดที่ 'ดีที่สุด' หรือ 'มากที่สุด' ของอะไรบางอย่างได้ยังไง? ไม่ว่าจะเป็นปริมาตรของกล่องที่ใหญ่ที่สุด, ความเร็วที่เหมาะสมที่สุด, หรือกำไรที่สูงสุด? วันนี้ Panya AI Tutor จะชวนมาค้นหาคำตอบด้วยเครื่องมือสุดเจ๋งอย่าง แคลคูลัส กัน!

บทความนี้จะพาเราไปดูกรณีศึกษาที่น่าสนใจ: การหาปริมาตรกล่องที่มากที่สุด จากกระดาษแผ่นเดียว!

💡 ปัญหาของเรา: กล่องปริมาตรสูงสุด

โจทย์: ถ้าเรามีกระดาษสี่เหลี่ยมจัตุรัสขนาด $L \times L$ แล้วตัดมุมออกเป็นสี่เหลี่ยมจัตุรัสเล็กๆ ขนาด $x \times x$ จากนั้นพับเป็นกล่องไม่มีฝา เราจะหาค่า $x$ ที่ทำให้กล่องมีปริมาตรมากที่สุดได้อย่างไร?
คำถามจากนักเรียน: "พอกล่องสูงขึ้น ฐานมันก็แคบลง ปริมาตรเลยลดลงตอนท้าย... แล้วเราจะใช้แคลคูลัสหาจุดที่ 'ปริมาตรเยอะที่สุด' นั้นแบบเป๊ะๆ ได้ยังไง โดยไม่ต้องมานั่งเดาค่า $x$?"

🛠️ ขั้นตอนที่ 1: สร้างฟังก์ชันปริมาตร $V(x)$

หัวใจสำคัญของการแก้ปัญหาด้วยแคลคูลัสคือการ เปลี่ยนปัญหาในชีวิตจริงให้เป็นสมการทางคณิตศาสตร์

สูตรปริมาตรพื้นฐาน: เราเริ่มต้นจากสูตรปริมาตรกล่อง: $$V = \text{กว้าง} \times \text{ยาว} \times \text{สูง}$$
ระบุตัวแปร: เราให้ $x$ เป็นความยาวด้านของสี่เหลี่ยมจัตุรัสที่ถูกตัดออกจากมุม ซึ่ง $x$ จะกลายเป็น ความสูงของกล่อง เมื่อพับขึ้นมา
หาความสัมพันธ์: เมื่อเราตัดมุมออก $x$ หน่วยจากแต่ละด้านของกระดาษขนาด $L \times L$:
- ความสูง (height) ของกล่อง = $x$
- ความกว้าง (width) ของฐาน = $L - 2x$
- ความยาว (length) ของฐาน = $L - 2x$
สร้างฟังก์ชันปริมาตร: แทนค่าลงในสูตรปริมาตร เราจะได้ฟังก์ชันปริมาตร $V(x)$ ในรูปของ $x$: $$V(x) = (L-2x)(L-2x)x$$ หรือเขียนใหม่ได้เป็น: $$V(x) = x(L-2x)^2$$
กำหนดขอบเขต (โดเมน) ของ $x$: $$0 \le x \le L/2$$

📈 ขั้นตอนที่ 2: ใช้ "อนุพันธ์" หาจุดสูงสุด

เราได้ฟังก์ชัน $V(x)$ มาแล้ว ทีนี้จะหาจุดสูงสุดได้อย่างไร? เครื่องมือวิเศษของเราคือ อนุพันธ์ (Derivative)!

ที่จุดสูงสุด (หรือต่ำสุด) ของกราฟ ความชันของกราฟ ณ จุดนั้นจะเป็นศูนย์เสมอ! (เหมือนยอดเขาที่พื้นราบเรียบ)

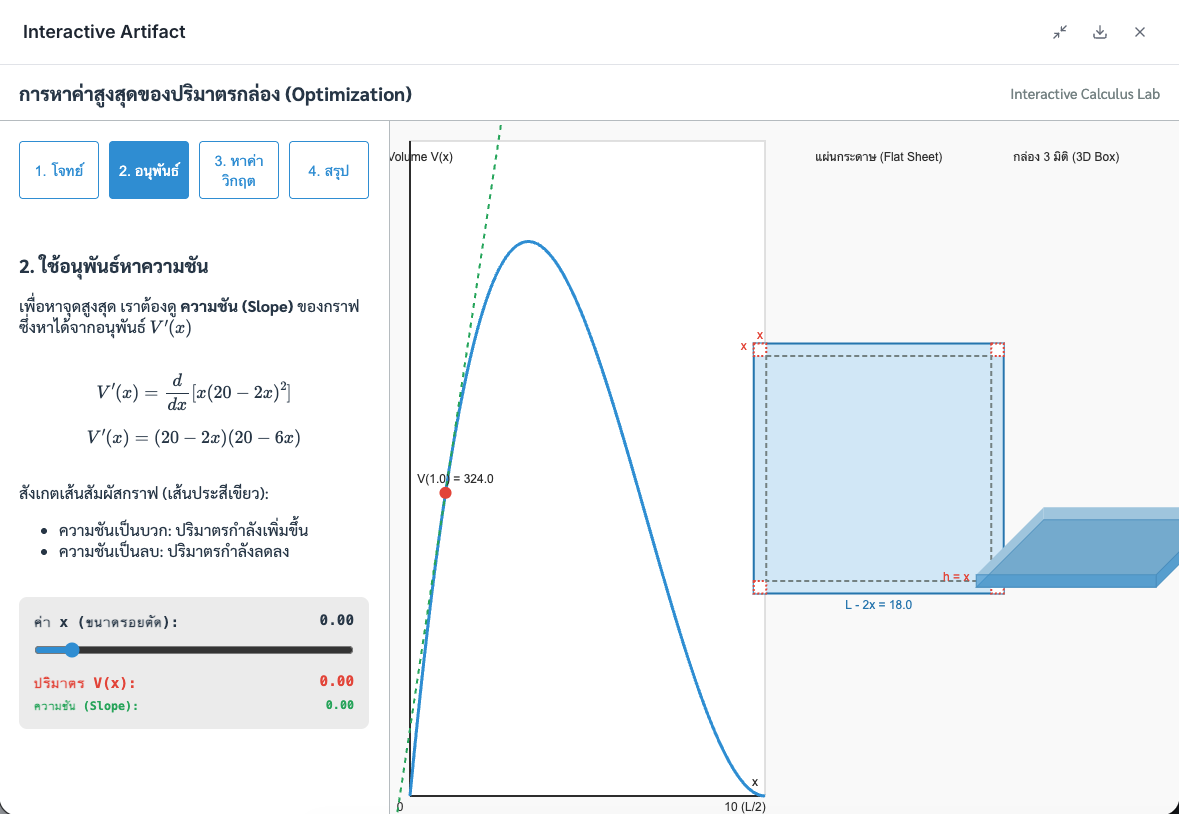
ทำไมต้องดิฟ?: ภาพนี้แสดงความหมายของ $V'(x)$ เส้นประสีเขียวคือ 'เส้นสัมผัสกราฟ' เป้าหมายของเราคือหาจุดที่เส้นนี้ 'ขนานกับพื้น' (ความชัน = 0)

ขั้นตอนที่ 2.1: หาอนุพันธ์อันดับหนึ่งของ $V(x)$

จากฟังก์ชัน $V(x) = x(L-2x)^2$ เราจะใช้ กฎการคูณ (Product Rule) และ กฎลูกโซ่ (Chain Rule):

$$V'(x) = (1)(L-2x)^2 + (x)(-4(L-2x))$$ $$V'(x) = (L-2x)^2 - 4x(L-2x)$$

ดึงตัวร่วม $(L-2x)$ ออกมา:

$$V'(x) = (L-2x)[(L-2x) - 4x]$$ $$V'(x) = (L-2x)(L-6x)$$

ขั้นตอนที่ 2.2: กำหนดให้อนุพันธ์เป็นศูนย์เพื่อหาค่าวิกฤต

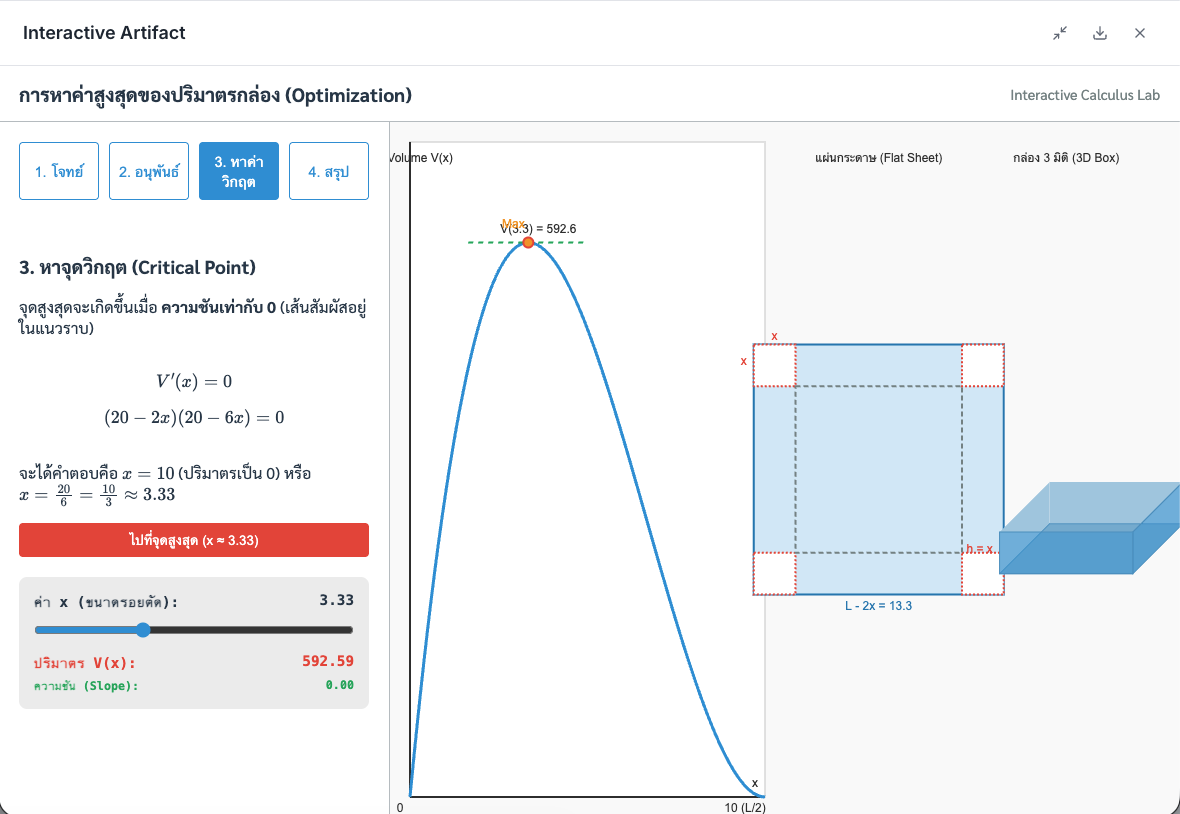
หาคำตอบที่แม่นยำ: แทนที่จะกะด้วยสายตา Panya AI Tutor ช่วยแสดงวิธีทำทีละขั้นตอน โดยการจับสมการ $V'(x) = 0$ แล้วแก้สมการหาค่า $x$

เมื่อเรากำหนดให้ความชันเป็นศูนย์ $V'(x) = 0$:

$$ (L-2x)(L-6x) = 0 $$

เราจะได้ค่า $x$ ที่เป็นไปได้สองค่าคือ $x = L/2$ และ $x = L/6$

ตรวจสอบคำตอบ: ที่ $x = L/2$ กล่องจะแบนแต๊ดแต๋ (ปริมาตรเป็น 0) ดังนั้นคำตอบที่ถูกต้องคือ $x = L/6$ ซึ่งเป็นจุดสูงสุดครับ

🎉 สรุปคำตอบ: ปริมาตรกล่องสูงสุด!

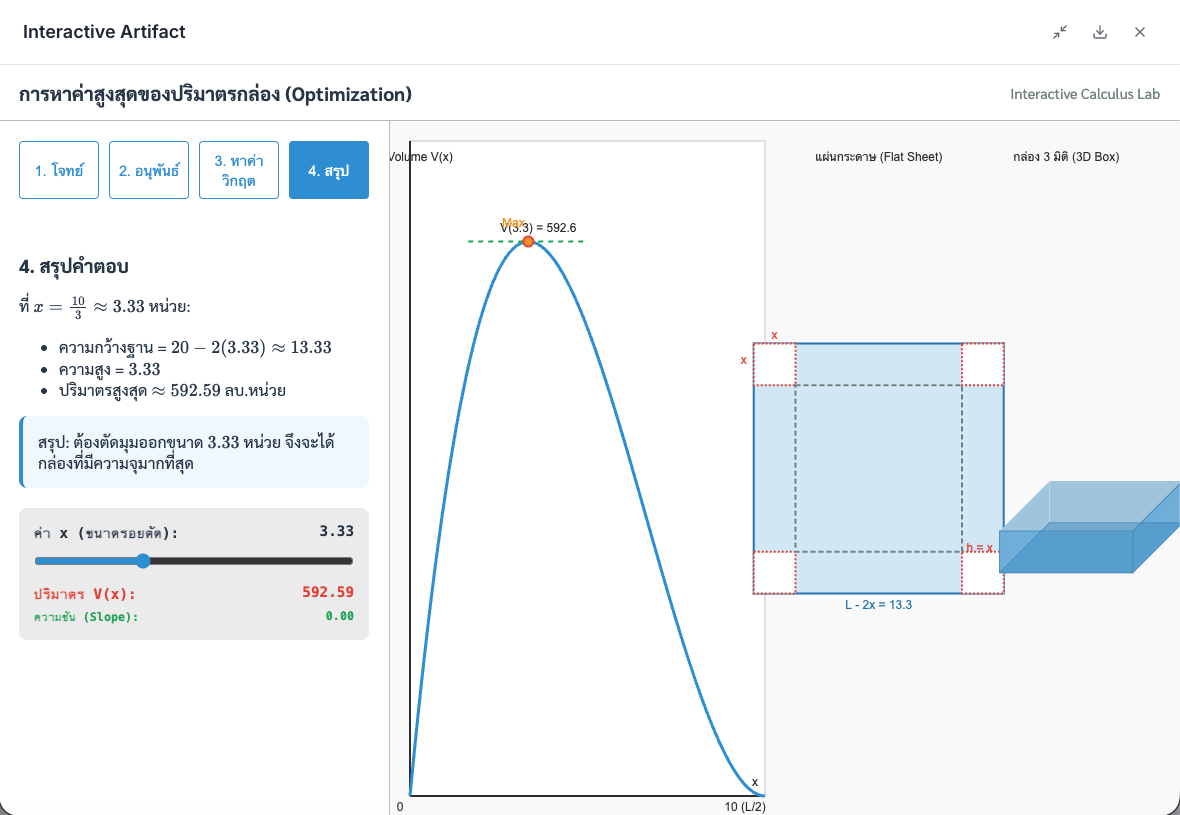
บทสรุป: เมื่อเราเลื่อนค่า $x$ ไปที่จุดที่คำนวณได้ จะเห็นว่าจุดสีส้มขึ้นไปแตะ 'ยอดดอย' ของกราฟพอดีเป๊ะ ยืนยันว่าแคลคูลัสถูกต้อง!

เพื่อให้ได้ปริมาตรกล่องที่มากที่สุด เราจะต้องตัดมุมกระดาษเป็นสี่เหลี่ยมจัตุรัสที่มีด้านยาว $x = L/6$ หน่วย

เมื่อแทนค่ากลับไปจะได้ปริมาตรสูงสุดคือ:

$$V_{max} = \frac{2L^3}{27}$$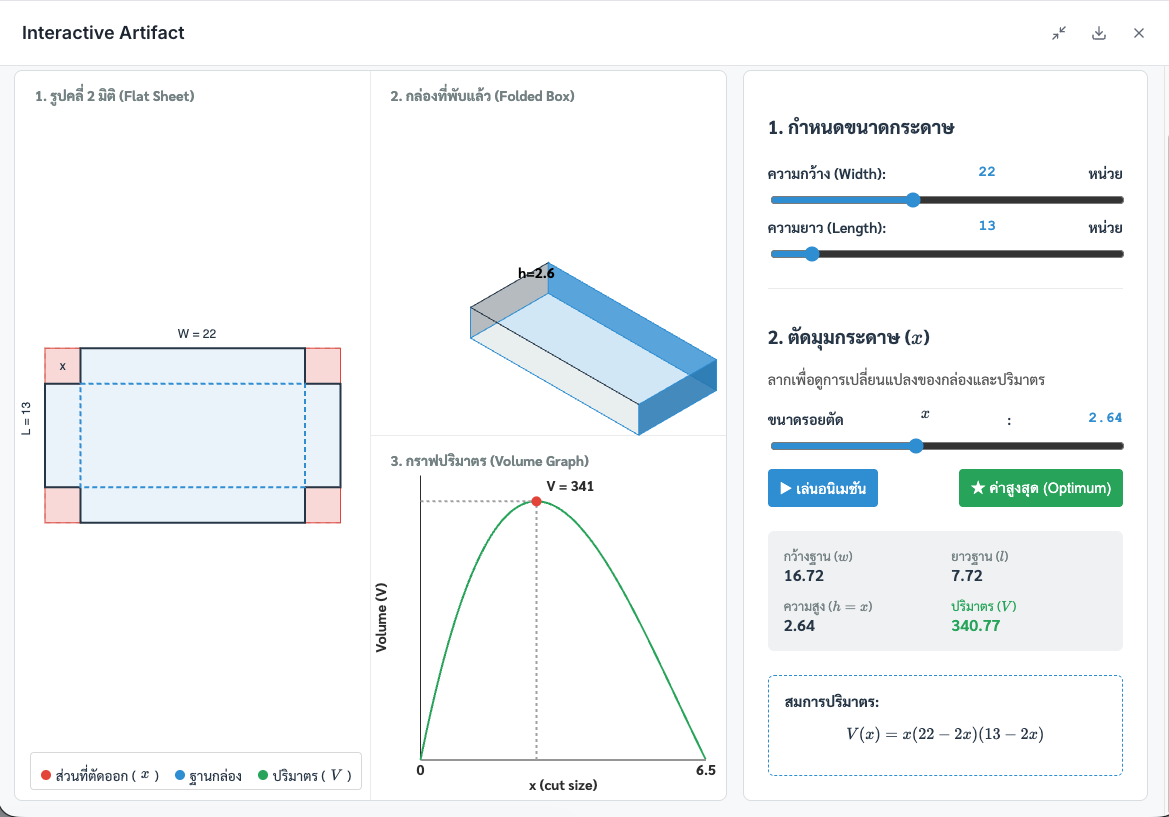

Interactive Sandbox: ไม่จำเป็นต้องเป็นสี่เหลี่ยมจัตุรัสเสมอไป! ลองเปลี่ยนขนาดกระดาษได้ตามโจทย์การบ้านเพื่อดูผลลัพธ์

อยากลองหมุนกล่องเล่น หรือลองเปลี่ยนโจทย์เป็นเลขอื่นไหม?

มาลองเล่น Interactive Math แบบนี้ได้ที่ Panya AI Tutor เลย!

ลองใช้งาน Panya AI Tutor ฟรี